For interpolating the value of the function y = f (x) near the end of table of values, and to extrapolate the value of the function a short distance forward from yn , Newton’s backward interpolation formula is used
Backward Differences:
The differences y1 – y0, y2 – y1, ……, yn – yn–1 are called first backward difference.
Thus Let us first construct the backward difference table for the given data:
Backward difference table
NEWTON’S GREGORY BACKWARD INTERPOLATION FORMULA :
Example: What will be the population in 1925 as per following data table.
X (Year)
|
1891
|
1901
|
1911
|
1921
|
1931
|
Y(Population)
|
46
|
66
|
81
|
93
|
101
|
Solution:
f(1925)=?
Backward difference table
here
hence
f(1925)=
101 +(-0.6)(8)+ [(-0.6)(0.4)(-4)]/!2 + [(-0.6)(0.4)(1.4)(-1)]/!3 +[(-0.6)(0.4)(1.4)(2.4)(-3)]/!4
=101-4.8+[(0.96)/2]+[(0.336)/6]+[(2.4192)/24]
=101-4.8+0.48+0.056+0.1008
=96.8368
C Program:
#include<stdio.h>
int fact(int);
void main()
{
int n,i,j,ch=30;
float arr[10][11],px=1,x,y,p,h;
printf("\nEnter the no of data:");
scanf("%d",&n);
printf("\nEnter the data:");
for(i=0;i<n;i++)
{
printf("\nX%d=",i+1);
scanf("%f",&arr[i][0]);
printf("\nY%d=",i+1);
scanf("%f",&arr[i][1]);
}
//forming the difference table
for(j=2;j<=n;j++)
{for(i=0;i<n-1;i++)
arr[i][j]=arr[i+1][j-1]-arr[i][j-1];
}
//printing table
printf("\nThe difference table");
printf("\n\tX \tY");
for(i=0;i<n-1;i++)
printf("\t%c^%d",ch,i+1);
for(i=0;i<n;i++)
{printf("\n");
for(j=0;j<n+1-i;j++)
printf("\t%.4f",arr[i][j]);
}
printf("\nEnter the value of x for f(x)");
scanf("%f",&x);
//calculate the value of f(x) for x
h=arr[n-1][0]-arr[n-2][0];
p=(x-arr[n-1][0])/h;
y=arr[n-1][1];
for(i=1;i<n;i++)
{
px=px*(p+(i-1));
y=y+(arr[n-1-i][i+1]*px)/fact(i);
}
printf("\nthe value of f(x) at x=%f is %f",x,y);
}
int fact(int n)
{ int f=1,i;
for(i=1;i<=n;i++)
f=f*i;
return f;
}
Output:
Enter the no of data:5
Enter the data:
X1=1891
Y1=46
X2=1901
Y2=66
X3=1911
Y3=81
X4=1921
Y4=93
X5=1931
Y5=101
The difference table
X Y ^1 ^2 ^3 ^4
1891.0000 46.0000 20.0000 -5.0000 2.0000 -3.0000
1901.0000 66.0000 15.0000 -3.0000 -1.0000
1911.0000 81.0000 12.0000 -4.0000
1921.0000 93.0000 8.0000
1931.0000 101.0000
Enter the value of x for f(x) 1925
the value of f(x) at x=1925.000000 is 96.836800


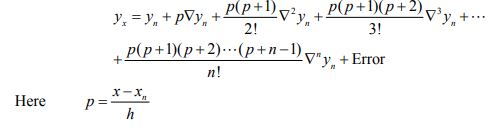


No comments:
Post a Comment